چند جمله ای ها در نرم افزار matlab
متلب، چند جمله ای ها را به صورت بردار سطری شامل ضرایب x ها به صورت نزولی (توان x) می نویسد. معادله P(x) = x4 + 7x3 - 5x + 9 به صورت p = [1 7 0 -5 9] نوشته می شود.
سرویس آموزش و آزمون برق نیوز: متلب، چند جمله ای ها را به صورت بردار سطری شامل ضرایب x ها به صورت نزولی (توان x) می نویسد. معادله P(x) = x4 + 7x3 - 5x + 9 به صورت p = [1 7 0 -5 9] نوشته می شود.
ارزیابی چند جمله ای ها
تابع polyval برای ارزیابی چند جمله ای ها در یک مقدار خاص استفاده می شود. برای مثال، تابع قبلی p را در نقطه x = 4 ارزیابی کنید.
p = [1 7 0 -5 9];
polyval(p,4)
متلب عبارت بالا اجرا کرده و نتیجه زیر را بر می گرداند.
ans = 693
همچنین تابع polyvalm برای ارزیابی چند جمله ای ماتریسی به کار می رود. چند جمله ای ماتریسی چند جمله ای است که متغیر هایش ماتریس می باشد.
مثال
ماتریس مربعی X را در نظر گرفته و چند جمله ای P را در X ارزیابی کنید.
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)
متلب عبارت بالا را اجرا کرده و نتیجه را به صورت زیر بر می گرداند.
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269
پیدا کردن ریشه های چند جمله ای
تابع roots، ریشه های چند جمله ای را محاسبه می کند. برای مثال ریشه های چند جمله ای P را بنویسید.
p = [1 7 0 -5 9];
r = roots(p)
r = roots(p)
متلب عبارت بالا را اجرا کرده و به صورت زیر بر می گرداند.
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095i
تابع poly معکوس تابع ریشه ها می باشد و ضرایب چند جمله ای را بر می گرداند. برای مثال
p2 = poly(r)
متلب عبارت بالا را اجرا کرده و نتیجه را بر می گرداند.
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000i
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000i
چندجمله ای برازش منحنی
تابع polyfit ضرایب یک چندجمله ای که یک مجموعه ای از داده ها را در کمترین مربعات برازش می کند. اگر X و Y دو بردار و چند جمله ای برازش از درجه n باشد، چندجمله ای برازش به صورت زیر نوشته می شود.
p = polyfit(x,y,n)
مثال
یک فایل اسکریپت ایجاد کرده و کد های زیر را در آن بنویسید.
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on
وقتی فایل اجرا شد، نتیجه به صورت زیر خواهد بود.
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250
و نمودار آن شکل زیر است.
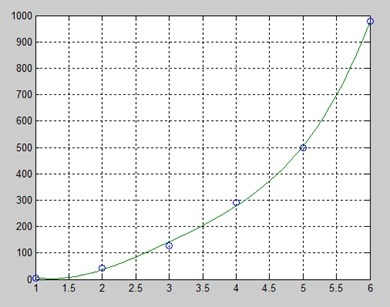
منبع: سایت تحلیل داده


از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.