تشریح معیار پایداری راث هرویتز به همراه مثال - بخش اول
معیار پایداری راث هرویتز، الگوریتم سادهای است که با استفاده از آن میتوان تعیین کرد که همه صفرهای یک چندجملهای در سمت چپ صفحه مختلط قرار دارند (گاهی چنین چندجملهای را هرویتز مینامند) یا خیر. چندجملهای هرویتز، یک التزام اساسی برای پایدار بودن (خروجی کراندار به ازای ورودی کراندار) یک سیستم تغییرناپذیر با زمان پیوسته خطی (LTI) است.
سرویس آموزش و آزمون برق نیوز، معیار پایداری راث هرویتز، الگوریتم سادهای است که با استفاده از آن میتوان تعیین کرد که همه صفرهای یک چندجملهای در سمت چپ صفحه مختلط قرار دارند (گاهی چنین چندجملهای را هرویتز مینامند) یا خیر. چندجملهای هرویتز، یک التزام اساسی برای پایدار بودن (خروجی کراندار به ازای ورودی کراندار) یک سیستم تغییرناپذیر با زمان پیوسته خطی (LTI) است.
شرط لازم پایداری
شرط لازم پایداری یک سیستم LTI، «هرویتز» (Hurwitz) بودن چندجملهای است. یعنی همه صفرهای چندجملهای در سمت چپ صفحه مختلط قرار داشته باشند. اگر حتی یکی از ریشهها در سمت راست صفحه مختلط باشند، چندجملهای پایدار نیست.
شرط کافی پایداری
شرایط کافی پایداری، شرایطی است که اگر برقرار باشد، چندجملهای پایدار خواهد بود. برای مثال، همانطور که خواهیم دید، شرط لازم و کافی یک سیستم LTI با معیار پایداری راث هرویتز، این است که همه درایههای ستوان اول آرایه راث همعلامت باشند.
معیار راث هرویتز
معیار راث هرویتز (Routh-Hurwitz Criterion)، هر دو شرط لازم و کافی را برای هرویتز بودن یک چندجملهای بیان میکند و شامل سه آزمون مجزا است که باید هر سه آنها برقرار باشد. اگر هر کدام از این آزمونها برقرار نباشد، سیستم پایدار نیست و نیازی به انجام آزمونهای دیگر نیست. به همین دلیل، آزمونها را از آسانترین به سختترین انجام میدهیم.
آزمون راث هرویتز برای مخرج تابع تبدیل سیستم، یعنی معادله مشخصه انجام میشود؛ برای مثال، در یک تابع تبدیل حلقه بسته با G. (S)در مسیر پیشِرو و حلقه فیدبک H. (s)، داریم:
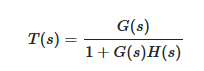
اگر این تابع تبدیل را ساده کنیم، یک کسر با صورت N. (s)و مخرج D. (s)خواهیم داشت:
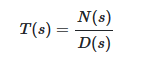
معیار پایداری راث هرویتز بر چندجملهای مخرج D. (s)اعمال میشود.
آزمونهای راث هرویتز
در اینجا، سه آزمون یا قاعده معیار راث هرویتز را بیان میکنیم. برای سادگی، فرض میکنیم درجه چندجملهای (بزرگترین توان s. در D. (s)) N. باشد. معادله D. (s)را میتوان به فرم عمومی زیر نوشت:
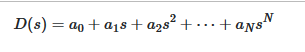
قاعده ۱: همه ضرایب aiباید غیرصفر باشند.
قاعده ۲: همه ضرایب aiباید مثبت باشند (یا همه آنها منفی باشند).
قاعده ۳: اگر قاعده ۱ و قاعده ۲، هر دو برقرار باشند، آنگاه آرایه راث را برای ضرایب ai تشکیل میدهیم. به ازای هر یک تغییر علامت در درایههای ستون اول آرایه راث، یک قطب در سمت راست صفحه s. وجود دارد (اگر تغییر علامت داشته باشیم، سیستم ناپایدار خواهد بود).
آرایه راث بهصورت زیر تشکیل میشود.
آرایه راث
آرایه راث با قرار دادن ضرایب aiچندجملهای D. (s)در کنار هم (و مطابق چینش زیر) تشکیل میشود. ستون آخر این آرایه را برابر صفر قرار میدهیم.
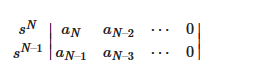
از آرایه بالا مشخص است که اگر N. فرد باشد، سطر اول فقط شامل ضرایب توانهای جملات فرد چندجملهای است و اگر N.
زوج باشد، ضرایب زوج، سطر اول را تشکیل میدهند.
از سطرهای بعدی (از سوم و بعد از آن) آرایه راث را به صورت زیر تکمیل میکنیم:

که در آن، ضرایب جدید به صورت زیر به دست میآیند:
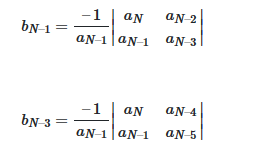
تکمیل آرایه را تا جایی ادامه میدهیم که به سطر s۰برسیم.
برای هر سطری که محاسبه میکنیم، درایه انتهایی سمت چپ سطر قبلی را عنصر محوری آن مینامیم. برای مثال، در سطر b.، عنصر محوری aN−۱ و در سطر c. عنصر محوری bN−۱است. برای به دست آوردن هر درایه، حاصل دترمینان زیر را قرینه کرده و بر عنصر محوری تقسیم میکنیم:
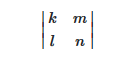
که در آن:
k. درایه انتهایی سمت چپ دو سطر بالاتر از سطر فعلی.
l. عنصر محوری.
m. درایه دو سطر بالاتر و ستون سمت راست ستون فعلی.
و n. درایه مشترک یک سطر بالاتر و یک ستون سمت راست درایه فعلی است.
معادله مربوط به درایه مورد نظر به صورت زیر است:
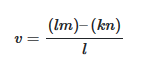
مثال ۱
در این مثال میخواهیم مقدار CN−۳را محاسبه کنیم. ابتدا باید مقادیر k، l، m. و n. را تعیین کنیم:
k. درایه انتهایی سمت چپ دو سطر بالاتر از سطر فعلی است: aN−۱
l. عنصر محوری و درایه انتهایی سمت چپ یک سطر بالاتر است: bN−۱
m. درایه دو سطر بالاتر و ستون سمت راست ستون فعلی است: aN−۵
n. داریه مشترک یک سطر بالاتر و یک ستون سمت راست درایه فعلی است: bN−۵
با قرار دادن مقادیر فوق در فرمول CN−۳، داریم:
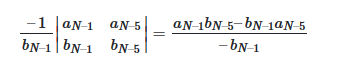
ادامه مقاله را تشریح معیار پایداری راث هرویتز به همراه مثال - بخش دوم ارائه می شود.


از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.