مدل موتور القایی در دستگاه DQ
یکی از مزایای تبدیل dq مجزاسازی پارامترها مدل ماشین میباشد که از این خاصیت میتوان برای اعمال استراتژی کنترل برای موتورها استفاده کرد.
سرویس آموزش و آزمون برق نیوز:
یکی از مزایای تبدیل dq مجزاسازی پارامترها مدل ماشین میباشد که از این خاصیت میتوان برای اعمال استراتژی کنترل برای موتورها استفاده کرد. در این قسمت ابتدا معادلات موتور القایی را بدست آورده و به سمت استاتور منتقل میکنیم. سپس با اعمال تبدیل dq بر روی معادلات، مدل موتور القایی را در دستگاه dq بدست میآوریم.
سیم پیچی استاتور و روتور موتور القایی متعادل با توزیع سینوسی را بصورت زیر در نظر بگیرید:
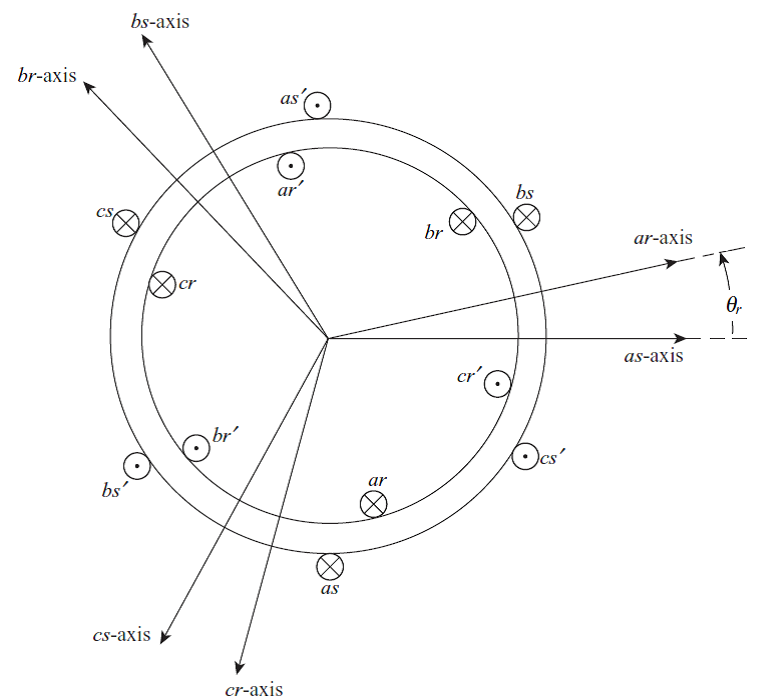
میتوان معادله ولتاژ استاتور و روتور را بصورت زیر نوشت:
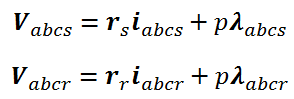
که اندیس s. مربوط به پارامترهای استاتور و r. مربوط به پارامترهای روتور میباشد و همچنین ماتریس متغیرها بصورت زیر میباشد:
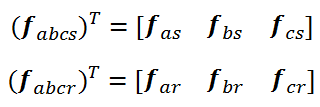
ماتریسهای rs و rr یک ماتریس قطری میباشند. برای سیستمهای خطی مغناطیسی، رابطه شار نشتی را بصورت زیر میتوان نوشت:
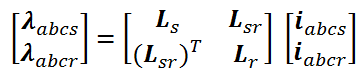
توجه کنید که Ls اندوکتانس نشتی بین سیم پیچیهای استاتور، Lr اندوکتانس نشتی بین سیم پیچیهای روتور و Lsr اندوکتانس متقابل بین سیم پیچیهای استاتور و روتور میباشد. این اندوکتانسها را میتوان بصورت زیر محاسبه کرد:
سیم پیچی استاتور و روتور موتور القایی متعادل با توزیع سینوسی را بصورت زیر در نظر بگیرید:

میتوان معادله ولتاژ استاتور و روتور را بصورت زیر نوشت:
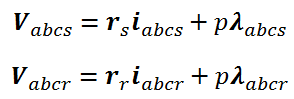
که اندیس s. مربوط به پارامترهای استاتور و r. مربوط به پارامترهای روتور میباشد و همچنین ماتریس متغیرها بصورت زیر میباشد:
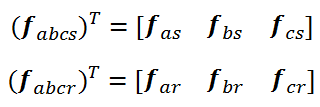
ماتریسهای rs و rr یک ماتریس قطری میباشند. برای سیستمهای خطی مغناطیسی، رابطه شار نشتی را بصورت زیر میتوان نوشت:
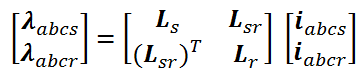
توجه کنید که Ls اندوکتانس نشتی بین سیم پیچیهای استاتور، Lr اندوکتانس نشتی بین سیم پیچیهای روتور و Lsr اندوکتانس متقابل بین سیم پیچیهای استاتور و روتور میباشد. این اندوکتانسها را میتوان بصورت زیر محاسبه کرد:
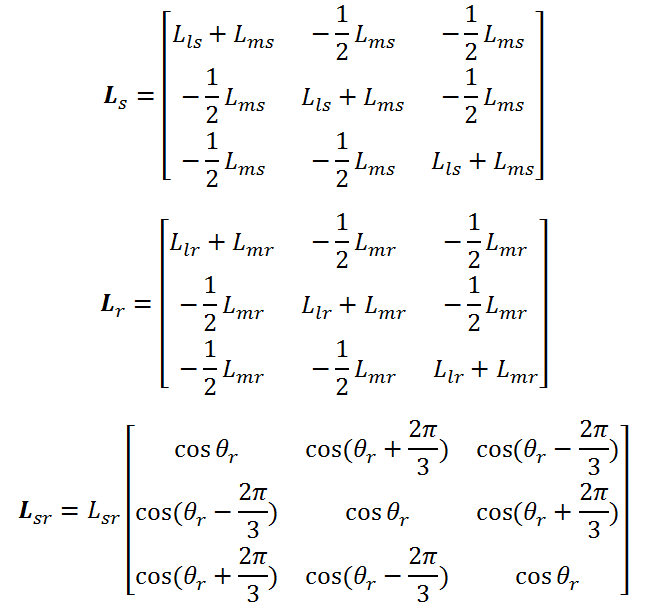
که Lls و Llr اندوکتانس نشتی و Lms و Lmr اندوکتانسهای متقابل میباشند. مثلاٌ، چون سیم پیچی فاز a. و b. با هم ۱۲۰ درجه اختلاف دارند بنابراین اندوکتانس بین سیم پیچی فاز a. استاتور و سیم پیچی فاز b. استاتور بصورت زیر میباشد:
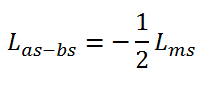
همان طور که از ماتریس اندوکتانس متقابل استاتور و روتور مشخص است، این ماتریس به سرعت روتور وابسته است و مولفههای این ماتریس با تغییر سرعت تغییر میکنند.
برای انتقال متغیرهای روتور به طرف استاتور با استفاده از نسبت دور سیم پیچیها داریم:
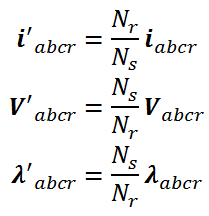
چون اندوکتانس مغناطیس کنندگی و متقابل هر دو دارای یک مسیر شار هستند پس میتوانیم بنویسیم:
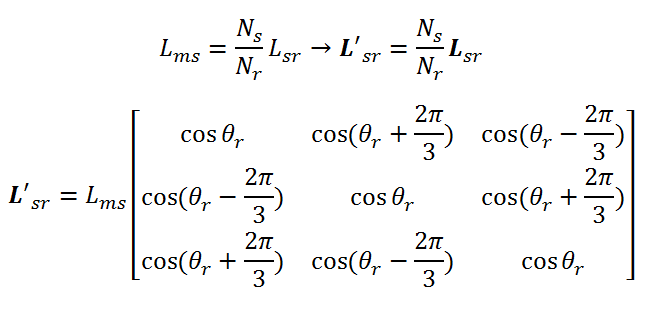
همچنین برای اندوکتانسهای روتور داریم:
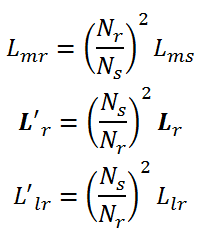
پس ماتریس اندوکتانس روتور منتقل شده به سمت استاتور بصورت زیر تبدیل میشود:
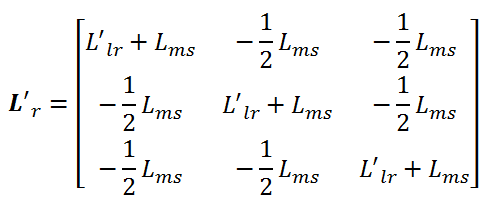
مقاومت انتقال یافته نیز بصورت زیر محاسبه میشود:
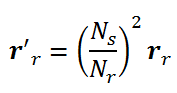
پس روابط ولتاژ منتقل شده به سمت استاتور بصورت زیر تبدیل میشوند:
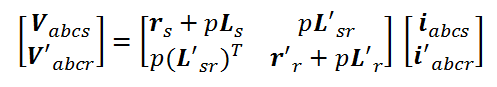
این مدل یک معادله دیفرانسیل درجه ۶ میباشد که ضرایب آن با سرعت روتور تغییر میکند؛ بنابراین با انتقال این مدل به قاب مرجع dq که با سرعت ω. میچرخد ضرایب معادلات دیفرانسیل ثابت میشوند. توجه کنید که سرعت ω. یک سرعت دلخواه میباشد و میتوان با مساوی قرار دادن آن با سرعت سنکرون، روتور و یا صفر مدلهای مختلف موتور القایی را در قاب مرجعهای سنکرون، روتور و ساکن بدست آورد.
با فرض سرعت دلخواه برای قاب مرجع dq و با توجه به شکل زیر داریم:
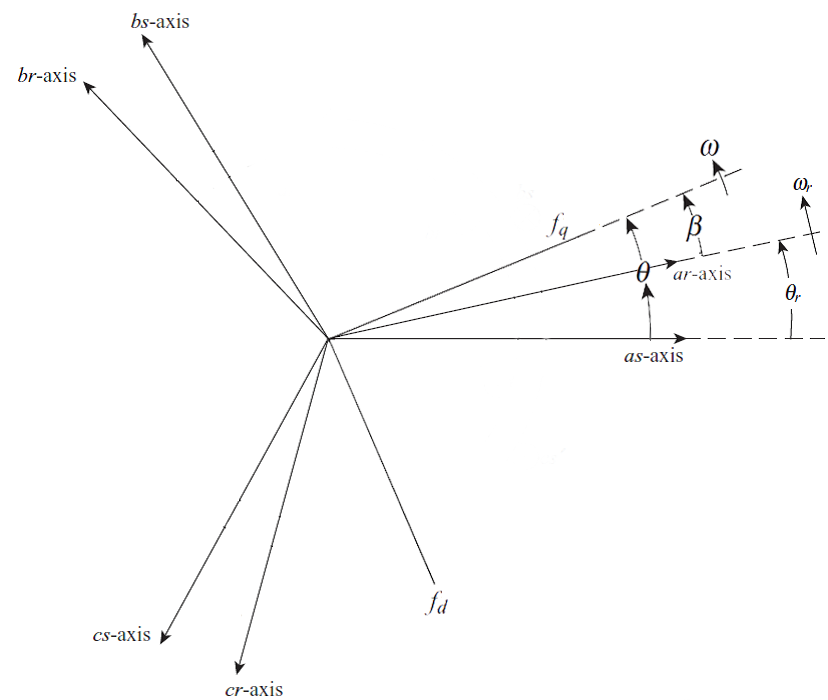
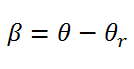
با توجه به شکل ماتریس انتقال dq برای انتقال پارامترهای استاتور به قاب مرجع dq عبارت است از:
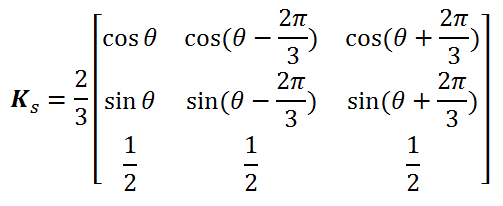
و ماتریس انتقال dq برای انتقال پارامترهای روتور به قاب مرجع dq عبارت است از:
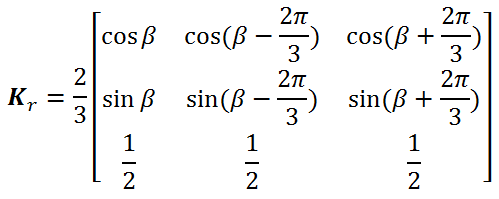
بنابراین با انتقال معادلات ولتاژ بدست آمده در بالا داریم:
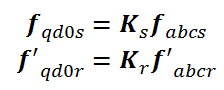
با ساده سازی روابط، معادلات ولتاژ در قاب مرجع dq بصورت زیر محاسبه میشوند:
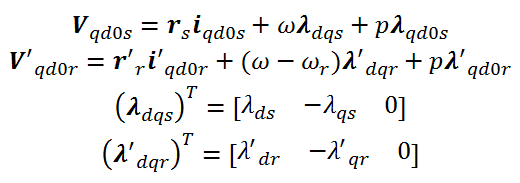
که قسمت اول مربوط به ولتاژ اهمی، قسمت دوم مربوط به ولتاژ حرکتی و قسمت سوم مربوط به ولتاژ ترانسفورمری میباشد.
شارهای نشتی نیز بصورت زیر محاسبه میشود:
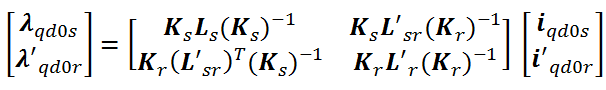
که هر یک از درایهها بصورت زیر محاسبه میشود:
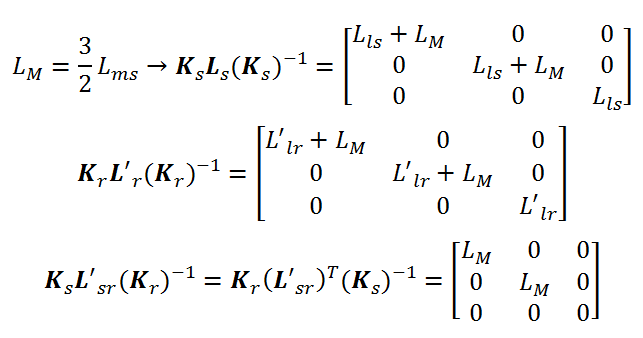
باز شدهی ماتریس معادلات ولتاژ dq بصورت زیر میباشد:
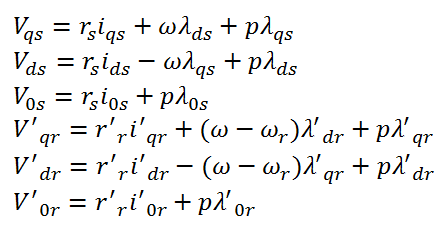
که مقادیر شار نشتی بصورت زیر محاسبه میشود:
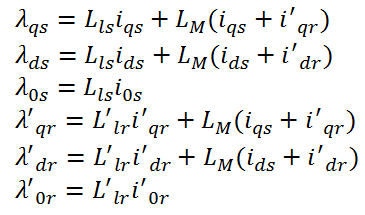
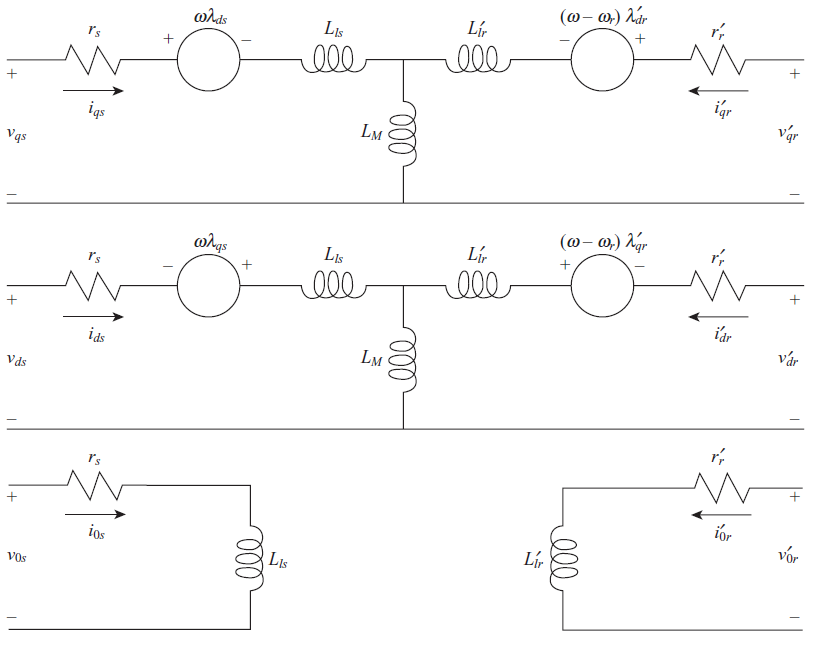
با استفاده از معادلات بالا میتوان مدل موتور القایی را بصورت زیر بدست آورد:



از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.