معرفی سیستم سه فاز - قسمت دوم

سرویس آموزش و آزمون برق نیوز،در این بخش، روابط اساسی ولتاژ و جریان مربوط به مدار‌های سه‌فاز با اتصال ستاره و مثلث را بیان خواهیم کرد.

تعاریف

ولتاژ‌های خط (که خط به خط نیز نامیده می‌شود)، ولتاژ بین خطوط هستند. بنابراین، EAB، EBC و ECA ولتاژ‌های خط به خط ژنراتور و Vab، Vbc و Vcaولتاژ‌های خط به خط بار هستند.

ولتاژ‌های فاز، ولتاژ فاز‌ها هستند. در یک بار Y، ولتاژ فاز، به‌عنوان اختلاف ولتاژ خط تا خنثی تعریف می‌شود (شکل ۷ (الف)). بنابراین، Van، Vbn و Vcn ولتاژ‌های فاز یک بار Y. هستند. برای بار Δ، فاز‌ها مطابق شکل ۷ (ب)، به‌صورت خط به خط بیان می‌شوند. همان‌طور که می‌بینیم، ولتاژ‌های فاز و خط در یک بار Δ. مشابه هستند. برای ژنراتور شکل ۷ (الف)، مقادیر EBN، EAN و ECNولتاژ فاز هستند.

جریان‌های خط، جریان‌هایی هستند که در هادی‌های خط می‌گذرند. برای نمایش این جریان، فقط از یک اندیس استفاده می‌کنیم. بنابراین، می‌توانیم از نماد‌های Ia، Ib و Ic در شکل ۷ یا IA، IB و IC در شکل ۴ استفاده کنیم. (البته گاهی از نماد‌هایی با دو اندیس نیز استفاده شده است، مانند IAa)

جریان‌های فاز، جریان‌هایی هستند که از فاز‌ها عبور می‌کنند. برای بار Y. شکل ۷ (الف)، جریان‌های Ia، Ib و Icاز امپدانس‌های فاز می‌گذرند و به همین دلیل، جریان فاز هستند.

امپدانس‌های فاز یک بار Y، امپدانس‌های بین a−n، b−n و c−n هستند (شکل ۷ (الف)) و با نماد‌های Zan، Zbn و Zcn نمایش داده می‌شوند. برای یک بار Δ. (شکل ۷ (ب))، امپدانس‌های فاز، Zab، Zbc و Zcaهستند. در یک بار متعادل، امپدانس همه بار‌ها با هم برابر است.

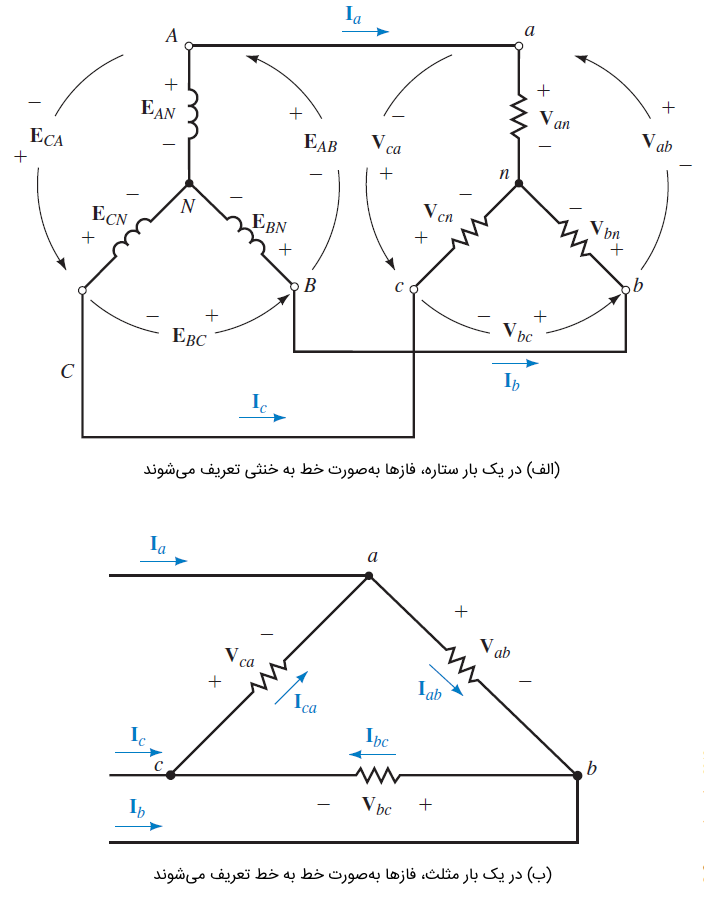
شکل ۷: نمادگذاری و نام‌گذاری ولتاژ‌ها و جریان‌های سه‌فاز

ولتاژ خط و فاز در یک مدار Y
در این قسمت، می‌خواهیم رابطه بین ولتاژ فاز و خط را در یک مدار ستاره پیدا کنیم. بدین منظور، شکل ۸ را در نظر بگیرید. با اعمال KVL، داریم: Vab−Van+Vbn=۰. بنابراین:

رابطه (۱)

اکنون فرض کنید بزرگی هر یک از ولتاژ‌ها V. باشد و Van را به‌عنوان مرجع در نظر بگیریم. بنابراین، Van=V∠۰∘ و Vbn=V∠−۱۲۰∘. با جایگذاری این دو مقدار در رابطه (۱)، داریم: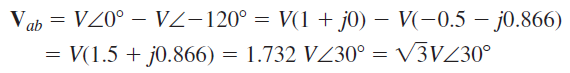



از طرفی می‌دانیم که Van=V∠۰∘. در نتیجه، رابطه زیر بین ولتاژ خط و ولتاژ فاز برقرار است:

رابطه (۲)

رابطه (۲) نشان می‌دهد که اندازه ولتاژ خط، سه برابر اندازه ولتاژ فاز است. همچنین، زاویه ولتاژ خط، به‌اندازه ۳۰∘از ولتاژ فاز جلوتر است. این موضوع، در شکل ۹ (الف) نشان داده شده است. برای دو فاز دیگر نیز روابط مشابه است (شکل ۹ (ب)). بنابراین، برای منبع می‌توان نوشت: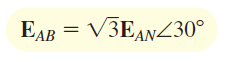

رابطه (۳)

شکل ۹: ولتاژ‌های یک بار ستاره متعادل

ولتاژ‌های نامی

ولتاژ خط خروجی ترانسفورماتور‌های توزیع برق، ۴۰۰ ولت است. مشترکان خانگی، معمولاً ولتاژ تک‌فاز استفاده می‌کنند و با رابطه‌ای که بیان کردیم و عدد ۴۰۰ ولت خط، مقدار ولتاژ فاز حدوداً ۲۳۰ ولت خواهد بود. این مقادیر را مقادیر نامی یا اسمی ولتاژ می‌نامند که استفاده از آن‌ها متداول است. احتمالاً ولتاژ ۲۲۰ ولت را بیشتر از ۲۳۰ ولت شنیده‌اید. هیچ‌کدام از این اعداد، اشتباه نیستند. ولتاژ ۲۳۰ ولت، مربوط به خروجی ترانسفورماتور است. به‌دلیلی تلفاتی که وجود دارد، این ولتاژ با اندازه حدود ۲۲۰ ولت به مصرف‌کننده می‌رسد.

با استفاده از معادلات (۲) و (۳)، می‌توان ولتاژ خط را با داشتن ولتاژ فاز محاسبه کرد: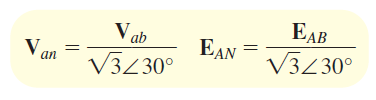

رابطه (۴)

با بیان موارد فوق، اکنون این توانایی را داریم که با داشتن هریک از شش ولتاژ خط یا فاز، سایر ولتاژ‌ها را حساب کنیم. این کار به‌راحتی و با ضرب یا تقسیم اندازه بر √۳و جابه‌جایی زاویه به‌انداره ۳۰∘انجام می‌شود.

جریان در مدار ستاره

همان‌طور که دیدیم، ولتاژ خط و فاز در یک بار ستاره، با هم برابر است. مطابق شکل ۱۰ (ب)، داریم: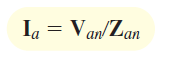

رابطه (۵)

برای Ibو Ic نیز روابط مشابهی برقرار است. از آن‌جایی که Vbn، Van و Vcn یک مجموعه متعادل را تشکیل می‌دهند، جریان‌های خط V، Ib و Icنیز یک مجموعه متعادل را شکل می‌دهند. بنابراین، با دانستن یکی از آن‌ها می‌توان دوتای دیگر را نیز به‌دست آورد.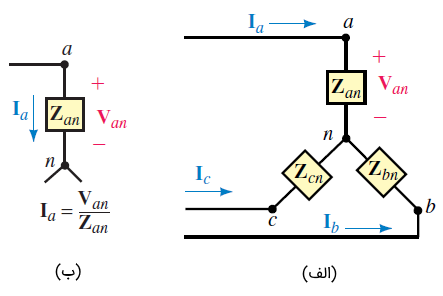

شکل ۱۰: تعیین جریان‌های بار ستاره

جریان‌های خط و فاز یک مدار مثلث

بار مثلث شکل ۱۱ را در نظر بگیرید. جریان فاز Iabرا می‌توان مطابق قسمت (ب) این شکل به‌دست آورد: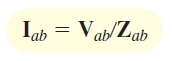

رابطه (۶)

با روابط مشابه می‌توان جریان‌های Ibcو Ica را نیز محاسبه کرد. از آن‌جایی که ولتاژ خطوط متعادل است، جریان‌های فاز نیز متعادل هستند. مجدداً شکل ۱۱ (الف) را در نظر بگیرید. با اعمال KCL در گره a. داریم: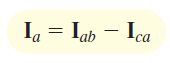

رابطه (۷)

با کمی محاسبات جبری، می‌توان رابطه زیر را نوشت: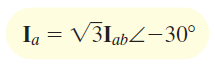

رابطه (۸)

بنابراین، اندازه Ia، برابر با √۳ برابر Iab است. همچنین، زاویه Ia، به‌اندازه ۳۰∘ از زاویه Iab جلوتر است. این گفته برای دو فاز دیگر نیز صادق است. بنابراین، در یک مدار مثلث، اندازه جریان خط، √۳ برابر اندازه اندازه جریان فاز است. همچنین، جریان هر خط، به‌اندازه ۳۰∘از جریان فاز متناظر آن عقب‌تر است. از آن‌جایی که جریان‌های فاز، متعادل هستند، جریان‌های خط نیز متعادل خواهند بود. این موضوع، در شکل ۱۱ (ج) نشان داده شده است. برای یافتن جریان‌های فاز با استفاده از جریان‌های خط، از رابطه زیر استفاده می‌کنیم: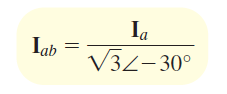

رابطه (۹)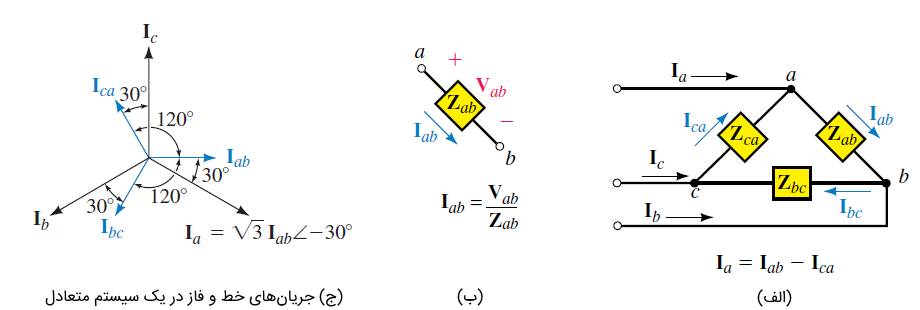

شکل ۱۱: جریان‌ها در یک بار مثلث

مدار معادل تک‌فاز

با توجه به نکاتی که گفتیم، واضح است اگر حل یک فاز سیستم سه‌فاز متعادل را داشته باشیم، می‌توانیم به‌سادگی کمیت‌های سه فاز دیگر را به‌دست آوریم. این گفته را می‌توان در قالب روش مدار معادل تک‌فاز برای سیستم‌های متعادل بیان کرد. یک سیستم Y-Y را با امپدانس خط در نظر بگیرید. سیستم ممکن است سه‌سیمه یا چهارسیمه با امپدانس هادی خنثی باشد. در هر دو حالت، از آن‌جایی که ولتاژ بین نقاط خنثی صفر است، می‌توان نقاط n. و N. را با یک هادی با امپدانس صفر به یک‌دیگر متصل کرد، بدون اینکه ولتاژ یا جریان در هر جای مدار دچار تغییر شود. این موضوع، در شکل ۱۲ (الف) نشان داده شده است.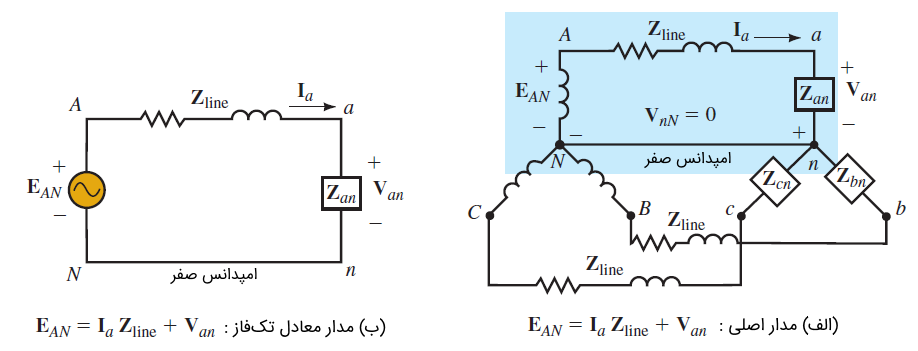

شکل ۱۲: مدار سه‌فاز و مدار معادل آن

مطابق شکل ۱۲ (ب)، می‌توان مدار فاز a. را جدا کرد. از آن‌جایی که VnN=۰ است، می‌توان گفت: معادله‌ای که فاز a. در مدار شکل ۱۲ (ب) را توصیف می‌کند، مشابه معادله‌ای است که در مدار اصلی وجود داشت. اگر بار Δ. داشته باشیم، آن را با استفاده از فرمول تبدیل Δ–Y برای بار‌های متعادل (ZY=ZΔ/۳) به بار Y. تبدیل می‌کنیم. این کار را می‌توان بدون توجه به پیکربندی یا پیچیدگی مدار انجام داد، زیرا مدار متعادل است.

انتخاب مرجع

قبل از آنکه مدار سه‌فاز را حل کنیم، باید یک مرجع انتخاب کنیم. برای مدار‌های Y، معمولاً EANیا Van را به‌عنوان مرجع در نظر می‌گیریم. برای مدار‌های Δ. نیز، معمولاً EAB یا Vabرا انتخاب می‌کنیم.

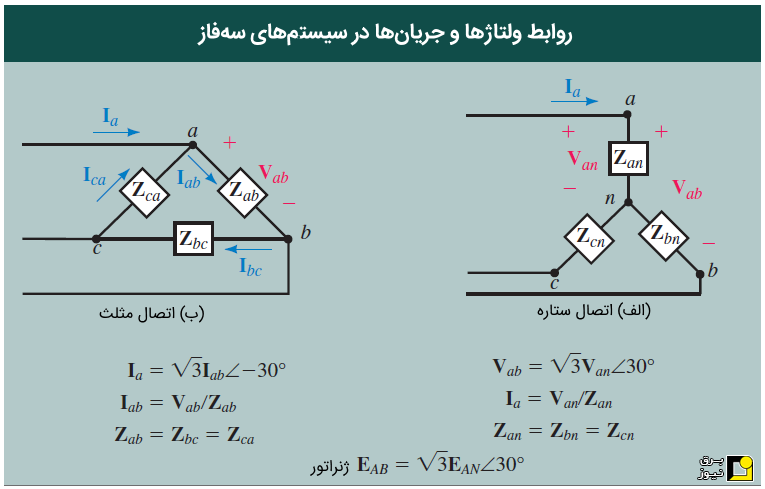
خلاصه روابط سه‌فاز اساسی

جدول زیر، خلاصه روابط اساسی در مدار‌های سه‌فاز را نشان می‌دهد. لازم به ذکر است که در سیستم‌های متعادل (ستاره یا مثلث)، همه ولتاژ‌ها و همه جریان‌ها متعادل هستند.

منبع: فرادرس