مدل موج سیار خط انتقال - بخش دوم
در مقاله قبلی مدل موج سیار را در حوزه زمان به دست آوردیم. یک راه دیگر برای بررسی مدل موج سیار، به دست آوردن آن در حوزه فرکانس و تبدیل آن به حوزه زمان است. همانطور که میدانیم، مدل پارامتر توزیع شده (حوزه فرکانس) حالت ماندگار که ولتاژ و جریان ابتدا و انتهای خط را به هم مربوط میکند.
سرویس آموزش و آزمون برق نیوز، بخش اول مقاله را می توانید از مدل موج سیار خط انتقال - بخش اول دانلود نمایید.
مدل موج سیار خطوط تکفاز با تلفات
مدل با پارامتر توزیع شده یک خط تکفاز به طول l متر در شکل ۵ نشان داده شده است.

شکل ۵: مدل خط با پارامتر توزیع شده تکفاز
با تحلیل مدار با استفاده از قوانین کیرشهف، مشابه آنچه برای خط بدون تلفات به دست آوردیم، خواهیم داشت:
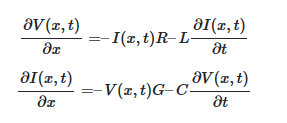
که در آن، G=۱/Rshرسانایی شنت است.
با مشتقگیری از معادله ولتاژ نسبت به xو معادله جریان نسبت به t، داریم:
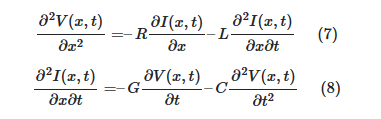
با جایگذاری معادله (۸) در معادله (۷)، خواهیم داشت:
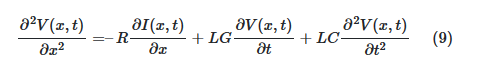
اگر در معادله بالا R=G=۰را قرار دهیم، آنگاه معادله موج خط انتقال مشابه با معادله (۵) در حالت بدون تلفات خواهد بود.
اگرچه با استفاده از فرمول دالامبر یک جواب عمومی برای خط بدون تلفات وجود دارد، اما برای خط دارای تلفات یک جواب به فرم بسته نداریم.
مدل با پارامتر توزیع شده یک خط تکفاز به طول l متر در شکل ۵ نشان داده شده است.

شکل ۵: مدل خط با پارامتر توزیع شده تکفاز
با تحلیل مدار با استفاده از قوانین کیرشهف، مشابه آنچه برای خط بدون تلفات به دست آوردیم، خواهیم داشت:
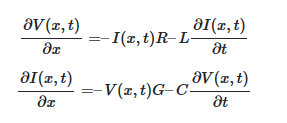
که در آن، G=۱/Rshرسانایی شنت است.
با مشتقگیری از معادله ولتاژ نسبت به xو معادله جریان نسبت به t، داریم:
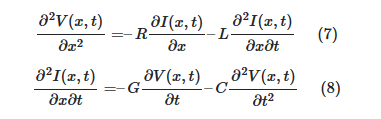
با جایگذاری معادله (۸) در معادله (۷)، خواهیم داشت:
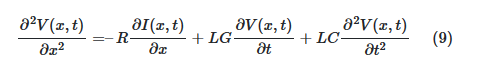
اگر در معادله بالا R=G=۰را قرار دهیم، آنگاه معادله موج خط انتقال مشابه با معادله (۵) در حالت بدون تلفات خواهد بود.
اگرچه با استفاده از فرمول دالامبر یک جواب عمومی برای خط بدون تلفات وجود دارد، اما برای خط دارای تلفات یک جواب به فرم بسته نداریم.
استخراج مدل موج سیار در حوزه فرکانس
در بخشهای قبلی، مدل موج سیار را در حوزه زمان به دست آوردیم. یک راه دیگر برای بررسی مدل موج سیار، به دست آوردن آن در حوزه فرکانس و تبدیل آن به حوزه زمان است. همانطور که میدانیم، مدل پارامتر توزیع شده (حوزه فرکانس) حالت ماندگار که ولتاژ و جریان ابتدا و انتهای خط را به هم مربوط میکند، به صورت زیر است:
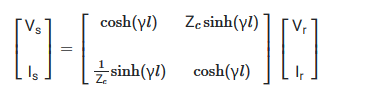
که در آن، γ=√zyثابت یا ضریب انتشار (m^−۱)، Zc=√z/y )امپدانس مشخصه برحسب اهم و z=R+jωl و y=G+jωC، به ترتیب، امپدانس سری و ادمیتانس شنت هستند.
با کمی عملیات جبری، معادلات حالت ماندگار بالا را میتوان به فرم زیر نوشت:
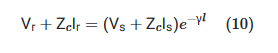
مدل حوزه زمان از تبدیل فوریه معکوس معادله (۱۰) به دست آورد.
در حالت بدون تلفات، (یعنی R=G=۰)، ضریب انتشار و امپدانس مشخصه به صورت زیر هستند:
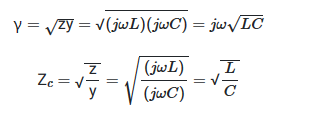
یکی از ویژگیهای عکس تبدیل فوریه این است که نماییهای مختلط در فضای فرکانس را به جابهجایی زمانی در حوزه زمان تبدیل میکند. بنابراین، با اعمال تبدیل فوریه معکوس به معادله (۱۰)، برای حالت بدون تلفات داریم:
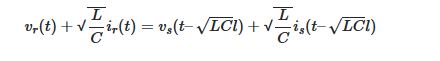
حالت بدون تلفات بالا نشان میدهد که مقادیر انتهای خط اساساً نسخههای جابهجا شده (گذشته) مقادیر ابتدای خط هستند که آنها را با استفاده از فرمول دالامبر به دست آوردیم.
در حالت کلیِ با تلفات، امپدانس مشخصه یک ثابت اسکالر نیست (اما تابعی از فرکانس است (Zc (ω))) و ثابت انتشار منجر به یک جابهجایی زمانی ساده در حوزه زمان نمیشود. بنابراین، معکوس تبدیل فوریه معادله (۱۰) به کانوولوشن منجر خواهد شد:
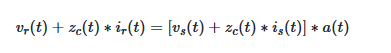
که در آن، (a (tمعکوس تبدیل فوریه e^−γ (ω)l و (zc (t عکس تبدیل فوریه (Zc (ω است. همانگونه که میتوان تصور کرد، انتگرالهای کانوولوشن در معادله بالا قابل حل نیستند.





از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.