مدل موج سیار خط انتقال - بخش آخر
در بخش آخر این مقاله به مدل موج سیار برای خطهایی با چند هادی و در انتها به جمع بندی مدل موج سیار خط انتقال پرداخته میشود.
سرویس آموزش و آزمون برق نیوز، بخشهای اول و دوم این مقاله را می توانید از مدل موج سیار خط انتقال - بخش اول و مدل موج سیار خط انتقال - بخش دوم مطالعه نمایید.
مدل موج سیار برای خطهایی با چند هادی
مدل موج سیار برای خطوط تکفاز بدون تلفات را میتوان با جایگزینی مقادیر ولتاژ و جریان با بردارهای n×۱برای n هادی بیان کرد. مثلاً برای یک خط سه فاز با سه هادی داریم:
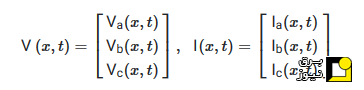
همچنین، اندوکتانس و ظرفیت (برحسب واحد طول) را میتوان با ماتریسهای n×nبرای نشان دادن کوپلینگ بین فازها نمایش داد. برای مثال، در یک خط سه فاز با سه هادی، خواهیم داشت:
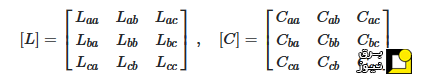
اکنون معادلات موج خط انتقال برای مدل تکفاز (معادلات (۵) و (۶) بالا) را میتوان برای مدل خط با چند هادی بازنویسی کرد:
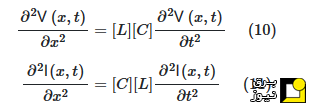
برخلاف حالت تکفاز، جواب عمومی برای معادلات دیفرانسیل مرتبه دوم (۱۰) و (۱۱) وجود ندارد، زیرا ضرب ماتریسی [L][C]معمولاً کامل است (یعنی درایههای غیر از قطر اصلی غیرصفر هستند). برای حل چنین معادلات دیفرانسیلی، یک تبدیل مدال برای دکوپلهسازی فازها لازم است.
بردارهای ولتاژ و جریان با ماتریسهای n×nتبدیلِ [Tv]و [Ti]از حوزه فاز به حوزه مدال تبدیل میشوند:
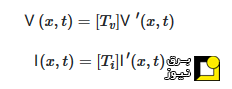
که در آن، (V′ (x,t)و (I′ (x,t)بردارهای ولتاژ و جریان مدال هستند:
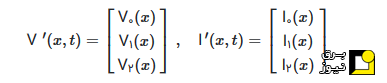
ماتریسهای تبدیلِ [Tv]و [Ti]به گونهای انتخاب میشوند که به ترتیب، بردارهای ویژه [L][C]و [C][L]باشند (مقادیر ویژه آنها یکسان است).
در حوزه مدال، معادلات (۱۰) و (۱۱) را میتوان به صورت مجموعهای از معادلات دکوپله بازنویسی کرد:
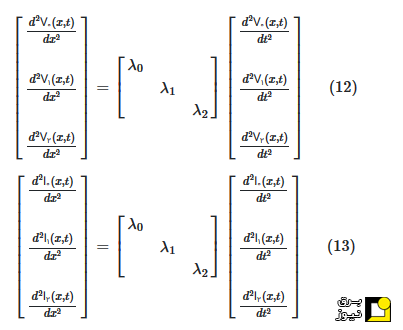
این معادلات دیفرانسیل مدال را میتوان به صورت تکی و با استفاده از فرمول دالامبر حل کرد. برای مثال، جواب برای حالت ۰
به صورت زیر است:
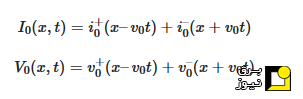
که در آن، v۰=۱√λ۰سرعت انتشار برای حالت ۰ و برحسب متر بر ثانیه است. همچنین، i+ (t) و i− (t) توابع جریان و v+ (t) و v− (t) توابع ولتاژ برای مد ۰هستند.
بعد از آنکه مقادیر حوزه مدال محاسبه شدند، آنگاه مقادیر حوزه فاز را میتوان با اعمال تبدیل معکوس به دست آورد.
در نهایت، باید این نکته را متذکر شد که جواب عمومی با استفاده تبدیل مدال فقط بر خطوط چندهادی بدون تلفات اعمال میشود. یک خط با تلفات موضوعاتی از قبیل جملات کوپلینگ دارد که موجب میشود نتوان از فرمول دالامبر استفاده کرد.
مدل موج سیار برای خطوط تکفاز بدون تلفات را میتوان با جایگزینی مقادیر ولتاژ و جریان با بردارهای n×۱برای n هادی بیان کرد. مثلاً برای یک خط سه فاز با سه هادی داریم:
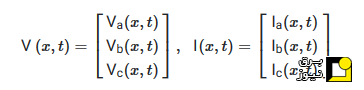
همچنین، اندوکتانس و ظرفیت (برحسب واحد طول) را میتوان با ماتریسهای n×nبرای نشان دادن کوپلینگ بین فازها نمایش داد. برای مثال، در یک خط سه فاز با سه هادی، خواهیم داشت:
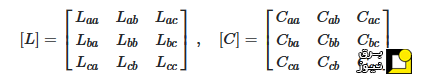
اکنون معادلات موج خط انتقال برای مدل تکفاز (معادلات (۵) و (۶) بالا) را میتوان برای مدل خط با چند هادی بازنویسی کرد:
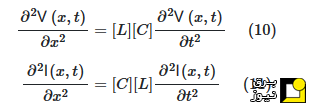
برخلاف حالت تکفاز، جواب عمومی برای معادلات دیفرانسیل مرتبه دوم (۱۰) و (۱۱) وجود ندارد، زیرا ضرب ماتریسی [L][C]معمولاً کامل است (یعنی درایههای غیر از قطر اصلی غیرصفر هستند). برای حل چنین معادلات دیفرانسیلی، یک تبدیل مدال برای دکوپلهسازی فازها لازم است.
بردارهای ولتاژ و جریان با ماتریسهای n×nتبدیلِ [Tv]و [Ti]از حوزه فاز به حوزه مدال تبدیل میشوند:
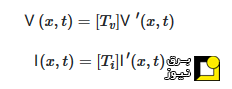
که در آن، (V′ (x,t)و (I′ (x,t)بردارهای ولتاژ و جریان مدال هستند:
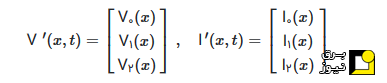
ماتریسهای تبدیلِ [Tv]و [Ti]به گونهای انتخاب میشوند که به ترتیب، بردارهای ویژه [L][C]و [C][L]باشند (مقادیر ویژه آنها یکسان است).
در حوزه مدال، معادلات (۱۰) و (۱۱) را میتوان به صورت مجموعهای از معادلات دکوپله بازنویسی کرد:

این معادلات دیفرانسیل مدال را میتوان به صورت تکی و با استفاده از فرمول دالامبر حل کرد. برای مثال، جواب برای حالت ۰
به صورت زیر است:
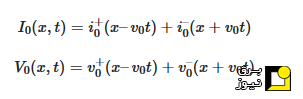
که در آن، v۰=۱√λ۰سرعت انتشار برای حالت ۰ و برحسب متر بر ثانیه است. همچنین، i+ (t) و i− (t) توابع جریان و v+ (t) و v− (t) توابع ولتاژ برای مد ۰هستند.
بعد از آنکه مقادیر حوزه مدال محاسبه شدند، آنگاه مقادیر حوزه فاز را میتوان با اعمال تبدیل معکوس به دست آورد.
در نهایت، باید این نکته را متذکر شد که جواب عمومی با استفاده تبدیل مدال فقط بر خطوط چندهادی بدون تلفات اعمال میشود. یک خط با تلفات موضوعاتی از قبیل جملات کوپلینگ دارد که موجب میشود نتوان از فرمول دالامبر استفاده کرد.
وابستگی پارامترهای خط به فرکانس
تاکنون اندوکتانس (L)، ظرفیت (C)، مقاومت (R) و هدایت (G) بر واحد طول پارامترهای خط را ثابت فرض کرده و برای محدودهای از فرکانسها به دست آوردیم. البته، این فرض معتبر نیست، خصوصاً در فرکانسهای بالاتر. برای مثال، اثر پوستی منجر به مقاومتهای بالاتر در فرکانسهای بالاتر میشود. بنابراین، صحیحتر این است که پارامترهای خط را وابسته به فرکانس بنویسیم؛ یعنی به صورت (L (ω)، C (ω)، R (ω) و (G (ω.
منبع: فرادرس





از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.