معادله نوسان ماشین سنکرون - بخش اول
برای کنترل فرکانس و بررسی پاسخ فرکانسی، داشتن مدل سیستم قدرت ضروری است. در این آموزش، معادله مهم ژنراتور سنکرون، موسوم به معادله نوسان ماشین سنکرون (Swing Equation) را به دست میآوریم.
سرویس آموزش و آزمون برق نیوز، برای کنترل فرکانس و بررسی پاسخ فرکانسی، داشتن مدل سیستم قدرت ضروری است. در این آموزش، معادله مهم ژنراتور سنکرون، موسوم به معادله نوسان ماشین سنکرون (Swing Equation) را به دست میآوریم. بدین منظور، از قانون دوم نیوتن برای یک جسم چرخان جهت استخراج معادله نوسان یک ژنراتور سنکرون و از فرضیاتی برای سادهسازی معادله استفاده خواهیم کرد. علاوه بر این، معادله خطی شده را برای آشفتگیهای سیگنالکوچک به دست خواهیم آورد. همچنین، با داشتن معادله نوسان، پاسخ فرکانسی دو سیستم مختلف را به تغییر بار یا تغییر توان مکانیکی بررسی میکنیم.
قانون نیوتن برای یک جسم چرخان
همانطور که گفتیم، معادله نوسان از قانون دوم نیوتن برای یک جسم چرخان به دست میآید. در یک ژنراتور سنکرون، جسم چرخان همان روتور است. قانون نیوتن بیان میکند که شتاب زاویهای متناسب با گشتاور خالص است:
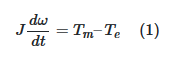
که در آن، Jلَختی روتور برحسب کیلوگرم در متر مربع (kg⋅m۲) یا ژول در ثانیه مربع (J⋅s۲) است. پارامتر ω سرعت چرخان برحسب rad/s، و گشتاورها برحسب واحد استاندارد نیوتن در متر (N⋅m) هستند. Tm گشتاور مکانیکی بار و Teگشتاور الکترومغناطیسی تولیدی میدان الکترومغناطیسی است.
مهندسان سیستم قدرت، اغلب از توان به جای گشتاور استفاده میکنند. بنابراین، رابطه بالا را برحسب توان مکانیکی Pm و توان الکتریکی Peتولیدی میدان الکترومغناطیسی مینویسیم.
همانطور که میدانیم، Pm=Tmωmکه در آن، ωm سرعت مکانیکی، و Pe=Te۲Pωe که در آن، ωe فرکانس مدار استاتور و P تعداد قطبهای ماشین است. برای ماشینهایی با دو قطب، رابطه Pe=Teωeبرقرار است.
در یک ژنراتور سنکرون با دو قطب، سرعت مکانیکی ωmو فرکانس الکتریکی ωe استاتور با هم برابرند. بنابراین، از ωبرای نمایش هر دو سرعت چرخش و فرکانس برق استفاده میکنیم. در نتیجه، معادله نوسان (۱) به صورت زیر در میآید:
توجه کنید که این معادله تنها به ماشینهای سنکرون قابل اعمال است. در ماشینهای القایی، Tm=Pm/ωm، و Te=Pe/ωe، که در آنها، ωm سرعت چرخش و ωe فرکانس الکتریکی در مدار استاتور است. در ماشینهای القایی، سرعت چرخش و فرکانس الکتریکی برابر نیستند. فرکانس الکتریکی ωe برابر با سرعت چرخش میدان مغناطیسی گردان یک ماشین دوقطب است و سرعت میدان برابر با مجموع سرعت مکانیکی ωm و فرکانس ωr جریان مدار روتور خواهد بود: ωe=ωm+ωr.
اگر اصطکاک و گشتاور اصطکاکِ متناسب با سرعت را در سیستم مکانیکی در نظر بگیریم، معادلات بالا به صورت زیر اصلاح خواهند شد:
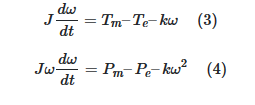
که در آنها، kضریب اصطکاک است.
معادله (۴) نسبت به عبارت ωغیرخطی است. هر دو Jωdωdt و kω۲غیرخطی هستند. بسط تیلور کاربرد فراوانی در به دست آوردن یک فرم خطی دارد. برای به دست آوردن یک بسط خطی، باید یک شرایط اولیه یا یک شرایط کار حالت مانا را در نظر بگیریم. در دینامیک و کنترل، شرایط حالت مانای اولیه و شرایط حالت مانای نهاییِ بعد از حالت گذار به عنوان نقاط تعادل شناخته میشوند.
معادله نوسان ماشین سنکرون حول سرعت نامی
اگر ژنراتور در شرایط نامی با سرعت ω۰کار کند، میتوانیم معادله بالا را با استفاده از بسط تیلور حول شرایط نامی خطیسازی کنیم. مدل خطی شده برای دینامیک سیگنالکوچک در حول شرایط نامی کاربرد دارد.
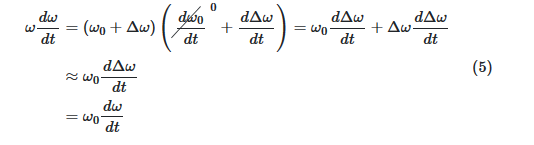
از آنجایی که ω۰ثابت است، dω۰/dt=۰ و Δωd/ dt)*Δω)حاصلضرب دو تغییر کوچک است که از آن چشمپوشی میکنیم.
خطیسازی جمله kω^۲مطابق روند کلی خطیسازی انجام شده است. برای تابع f (x)، انحراف یا تغییر کوچک در نقطه x۰ به صورت زیر بیان میشود:
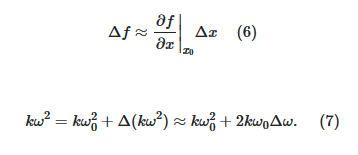
که در آن، Δω=ω–ω۰. قانون نیوتن برای شرایط حول نقطه کار نامی به صورت زیر در میآید:
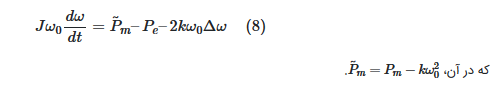
اگر ژنراتور در شرایط نامی با سرعت ω۰کار کند، میتوانیم معادله بالا را با استفاده از بسط تیلور حول شرایط نامی خطیسازی کنیم. مدل خطی شده برای دینامیک سیگنالکوچک در حول شرایط نامی کاربرد دارد.
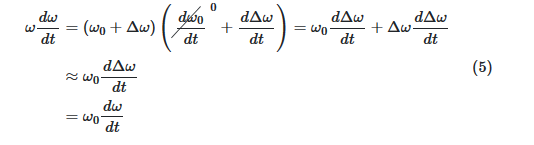
از آنجایی که ω۰ثابت است، dω۰/dt=۰ و Δωd/ dt)*Δω)حاصلضرب دو تغییر کوچک است که از آن چشمپوشی میکنیم.
خطیسازی جمله kω^۲مطابق روند کلی خطیسازی انجام شده است. برای تابع f (x)، انحراف یا تغییر کوچک در نقطه x۰ به صورت زیر بیان میشود:
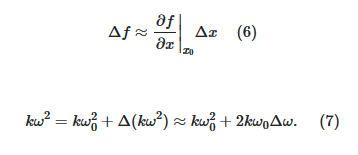
که در آن، Δω=ω–ω۰. قانون نیوتن برای شرایط حول نقطه کار نامی به صورت زیر در میآید:
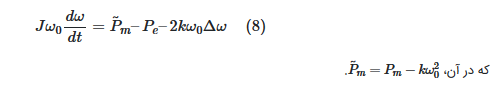



از ارسال دیدگاه های نا مرتبط با متن خبر، تکرار نظر دیگران، توهین به سایر کاربران و ارسال متن های طولانی خودداری نمایید.
لطفا نظرات بدون بی احترامی، افترا و توهین به مسئولان، اقلیت ها، قومیت ها و ... باشد و به طور کلی مغایرتی با اصول اخلاقی و قوانین کشور نداشته باشد.
در غیر این صورت، «برق نیوز» مطلب مورد نظر را رد یا بنا به تشخیص خود با ممیزی منتشر خواهد کرد.